Limit fungsi

Limit Fungsi Aljabar

Limit fungsi aljabar adalah salah satu konsep dasar yang ada di dalam kalkulus dan analisis, mengenai kelakuan sebuah fungsi yang mendekati titik masukan tertentu.

Sebuah fungsi memetakan keluaran f(x) untuk masing-masing masukan x. Fungsi tersebut mempunyai limit L pada titik masukan p bila f(x) “dekat” pada L ketika x dekat pada p.

Sehingga dengan sebutan lain, f(x) akan semakin dekat terhadap L pada saat x juga mendekat ke arah p.

Lebih jauh lagi, jika f diterapkan terhadap masing-masing masukan yang cukup dekat pada p, hasilnya merupakan keluaran yang (secara sembarang) dekat dengan L.

Jika masukan yang dekat pada p ternyata dipetakan pada keluaran yang sangat berbeda maka fungsi f akan disebut tidak mempunyai limit.

Definisi limit telah dirumuskan secara formal sejak abad ke-19.

Konsep Limit Fungsi Aljabar

Limit bisa kita definisikan sebagai menuju suatu batas, sesuatu yang dekat tetapi tidak bisa di raih.

Dalam bahasa matematikanya, kondisi tersebut bisa disebut sebagai limit.

Mengapa harus ada limit? Sebab limit mengungkapkan sebuah fungsi apabila ada batas tertentu didekati.

Mengapa harus didekati? Sebab sebuah fungsi pada umumnya tidak terdefinisi dalam titik-titik tertentu.

Meskipun sebuah fungsi seringkali tidak diartikan pada titik tertentu, tetapi masih bisa dicari tahu berapa nilai yang didekati oleh fungsi tersebut jika titik tertentu semakin didekati yakni dengan limit.

Dalam bahasa matematika, limit ditulis seperti berikut ini:

Artinya, jika x mendekati a tetapi x tidak sama dengan a maka f(x) akan mendekati L. Pendekatan x ke a bisa kita lihat dari dua sisi yakni sisi kiri dan juga sisi kanan atau dengan kata lain x bisa mendekati dari arah kiri dan arah kanan sehingga akan menghasilkan limit kiri dan limit kanan.

Sehingga, dari uraian di atas akan kita peroleh contoh rumus di bawah ini:

Untuk nilai x yang mendekati 1:

Berikut untuk gambar grafiknya:

Melihat dari gambar grafik di atas maka dapat diuraikan menjadi:

• Jika x mendekati 1 dari kiri, maka nilai f(x) mendekati 2 
  

• Jika x mendekati 1 dari kanan, maka nilai f(x) mendekati 2 
  

• Sehingga, jika x mendekati 1, maka nilai dari f(x) akan mendekati 2     

    

Toerema atau Pernyataan

Sebuah fungsi disebut mempunyai limit jika di antara limit kiri dan limit kananya memiliki besar nilai yang sama. Sehingga, jika limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.

Definisi dan Teorema Limit. Seperti yang telah diuraikan di atas, limit dalam bahasa umum berarti batas.

Pada saat kita belajar matematika ada beberapa guru yang menyebutkan jika limit adalah suatu pendekatan.

Artian dari limit ini menyebutkan bahwa sebuah fungsi f(x) akan mendekati nilai tertentu apabila x mendekati nilai tertentu.

Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut dengan epsilon dan delta.

Hubungan ke-2 bilangan positif kecil ini akan terangkum dalam definisi limit.

Sifat-sifat Limit Fungsi Aljabar

Jika n adalah suatu bilangan bulat positif, k konstanta, f dan g merupakan suatu fungsi yang memiliki limit di c, maka beberapa sifat di bawah ini akan berlaku.

Macam-macam Metode Penyelesaian Limit Aljabar

Ada beberapa metode atau cara penyelesaian untuk limit aljabar, diantaranya yaitu:

• Metode subitusi
• Metode pemfaktoran
• Metode membagi dengan pangkat tertinggi penyebut
• Metode mengalikan dengan faktor sekawan

Berikut akan kami jelaskan metodenya satu per satu. Simak baik-baik ya.

Menentukan Nilai Limit Fungsi Aljabar

Terdapat 2 jenis untuk menentukan limit fungsi aljabar, diantaranya yakni:

Bentuk yang pertama:

Serta bentuk yang kedua yaitu:

1. Metode Subsitusi

Metode subsitusi hanya akan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya.

Sebagai contoh:

Sehingga nilai fungsi limit aljabarnya yaitu:

2. Metode Pemfaktoran

Metode pemfaktoran digunakan apabila metode atau cara subsitusi yang menghasilkan nilai limit tidak bisa terdefinisikan.

Sebagai contoh:

Metode pemfaktoran digunakan dengan cara menentukan faktor persekutuan antara pembilang dan penyebutnya.

Dengan hubungannya terhadap bentuk limit kedua terdapat beberapa metode dalam menentukan nilai limit fungsi aljabar yakni metode atau cara membagi dengan pangkat tertinggi penyebut serta metode mengalikan dengan faktor sekawan.

3. Metode Membagi Pangkat Tertinggi Penyebut

Sebagai contoh:

Tentukanlah nilai limit fungsi aljabar dari limit di bawah ini:

Besar pangkat pembilang serta penyebut dalam soal yakni 2, sehingga,

Sehingga, nilai limit fungsi aljabar tersebut yaitu

Contoh soal 2.

Tentukan nilai limit fungsi aljabar dari limit di bawah ini:

Besar pangkat pembilang dan penyebut dalam soal adalah 3, sehingga,

Jadi, nilai dari limit fungsi aljabar tersebut adalah:

4. Metode Mengalikan Dengan Faktor Sekawan

Metode ini dipakai apabila dalam metode substitusi akan langsung menghasilkan nilai limit yang irasional.

Fungsi akan dikalikan dengan akar sekawannya supaya bentuk limit tersebut tidak irasional, sehingga dapat dilakukan kembali substitusi langsung nilai x → c .

Sebagai Contoh:

Limit Fungsi Aljabar Tak Hingga

Dalam pengoprasian limit fungsi aljabar, terkadang juga terdapa nilai x yang mendekati tak berhingga (∞).

Maka dari itu, apabila disubstitusikan fungsinya akan menghasilkan nilai yang tidak menentu.

Dalam pengoperasian limitnya, ada beberapa hukum atau teorema limit yang perlu kalian perhatikan. Apabila n merupakan bilangan bulat, k konstanta, fungsi f dan fungsi g merupakan fungsi-fungsi yang mempunyai nilai limit yang mendekati bilangan c, maka:

Dan terdapat dua metode dalam menyelesaikan limit fungsi aljabar bentuk tak berhingga, antara lain:

1. Membagi dengan pangkat tertinggi

Metode ini dipakai dalam limit fungsi bentuk .

Cara atau metode ini bisa dilakukan dengan cara membagi pembilang f(x) dan penyebut g(x) dengan variabel xn berpangkat tertinggi yang terdapa di dalam fungsi  f(x) dan g(x). Dan kemudian, baru bisa kita substitusikan dengan x → ∞.

Sebagai contoh:

2. Mengalikan bentuk sekawan

Metode ini dipakai pada limit fungsi bentuk . Metode atau cara ini bisa diselesaikan dengan perkalian bentuk sekawan, yaitu:

Lalu dilanjutkan dengan pembagian dengan metode pertama yakni membagi dengan pangkat tertinggi.

Sebagai contoh:

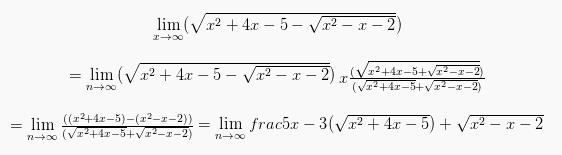
Berikutnya pembilang dan penyebut dibagi pada x pangkat tertinggi yakni x1:

Limit Fungsi Trigonometri

Limit juga bisa dipakai dalam fungsi trigonometri. Penyelesaiannya sama dengan fungsi limit aljabar. Tetapi, supaya paham mengenai penjalasan selanjutnya kalian harus mengerti terlebih dahulu konsep dari trigonometri.

Penyelesaian dalam limit fungsi ini pada trigonometri dapat digunakan dengan cara melakukan beberapa perubahan bentuk sinus, cosinus, dan tangen.

Terdapat tiga bentuk umum dalam limit fungsi trigonometri, diantaranya adalah:

1. Bentuk 

Dalam bentuk ini, limit dari fungsi trigonometri f(x) adalah hasil dari substitusi nilai c ke dalam x dari trigonometri.

Sebagai contoh:

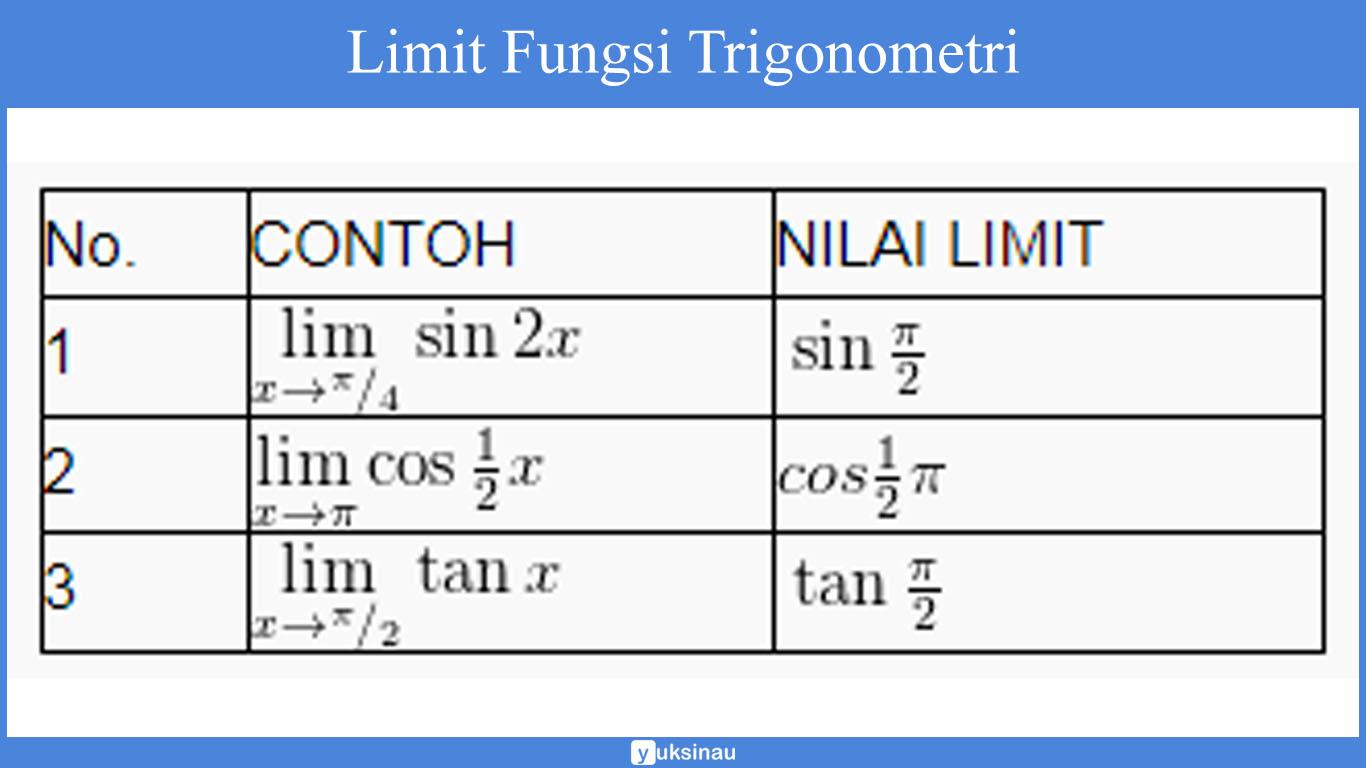
Apabila c = 0, maka rumus limit-limit trigonometrinya yaitu seperti berikut ini:

2. Bentuk 

Dalam bentuk ini, limit akan didapatkan dari perbandingan 2 trigonometri berbeda.

Kedua trigonometri tersebut apabila langsung disubstitusi dengan nilai c, maka akan menghasilkan f(c) = 0 dan g(c) = 0.

Sehingga, nilai limit trigonometri itu menjadi bilangan tak tentu . Penyelesaiannya sama dengan yang ada pada limit fungsi aljabar yakni pemfaktoran.

Contoh bentuk ini yakni:

3. Bentuk 

Dalam bentuk ini, limit didapatkan dari perbandingan antara trigonometri dan fungsi aljabar.

Apabila disubstitusikan langsung akan menghaslikan bilangan tak tentu. Dalam bentuk ini dikerjakan dengan konsep turunan. Bentuk rumus dasar limit ini yaitu:

Berdasarkan pada rumus dasar di ataas, apabila dikembangkan lagi akan menjadi rumus-rumus seperti di bawah ini: