aplikasi turunan ( garis singgung) tugas 8

Gradien Garis disimbolkan dengan m$$ dimana :

• gradien pada persamaan garis y=mx+c$$ adalah m$$
• gradien pada persamaan garis ax+by=c$$ adalah m=−ab$\frac{}{}$
• gradien jika diketahui dua titik (x1,y1)$\mathrm{}\mathrm{}$ dan (x2,y2)$\mathrm{}\mathrm{}$ adalah m=y2−y1x2−x1$\frac{{}_{\mathrm{}}{}_{\mathrm{}}}{{}_{\mathrm{}}{}_{\mathrm{}}}$

Gradien dua garis lurus :

• yang saling sejajar maka m1=m2${}_{\mathrm{}}{}_{\mathrm{}}$
• yang saling tegak lurus maka m1.m2=−1${}_{\mathrm{}}{}_{\mathrm{}}\mathrm{}$

Persamaan Garis Lurus :

• Jika diketahui satu titik (x1,y1)$\mathrm{}\mathrm{}$ dan gradien m$$, maka persamaan garisnya : y−y1=m(x−x1)${}_{\mathrm{}}{}_{\mathrm{}}$
• Jika diketahui dua titik (x1,y1)$\mathrm{}\mathrm{}$ dan (x2,y2)$\mathrm{}\mathrm{}$ maka persamaan garisnya : y−y1y2−y1=x−x1x2−x1$\frac{{}_{\mathrm{}}}{{}_{\mathrm{}}{}_{\mathrm{}}}\frac{{}_{\mathrm{}}}{{}_{\mathrm{}}{}_{\mathrm{}}}$

Nah materi dasarnya di atas jangan sampai terlupa yah, sekarang kita masuk materi yang sesungguhnya…hehehe…

Perhatikan Gambar Grafik fungsi y=f(x)$$

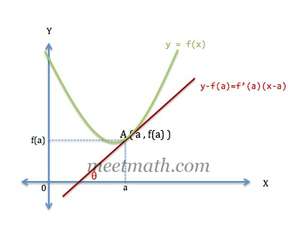
Kemiringan (gradien) garis singgung kurva y=f(x)$$ di titik A(a,f(a))$$ adalah

m=f′(a)=limΔx→0f(a+Δx)−f(a)Δx${}^{}\underset{\mathrm{}\mathrm{}}{}\frac{\mathrm{}}{\mathrm{}}$

Persamaan garis lurus yang melalui titik (x1,y1)$\mathrm{}\mathrm{}$ dengan gradien m$$ adalah y−y1=m(x−x1)${}_{\mathrm{}}{}_{\mathrm{}}$ , sehingga

Persamaan Garis Singgung di titik (a,f(a))$$ pada kurva adalah

y−f(a)=f′(a)(x−a)${}^{}$

ayooo langsung kita praktikkan…

1. Tentukan persamaan garis singgung kurva y=x2${}^{\mathrm{}}$ di titik (−1,1)$\mathrm{}\mathrm{}$ !
   Jawab :
   • cari m$$ dulu di x=−1$\mathrm{}$
     mm====f′(a)2x2(−1)−2$$\begin{array}{rcl}& & {}^{}\\ & & \mathrm{}\\ & & \mathrm{}\mathrm{}\\ & & \mathrm{}\end{array}$$
   • maka persamaan garris singgung kurva dengan gradien m=−2$\mathrm{}$ di (−1,1)$\mathrm{}\mathrm{}$ adalah:
     y−y1y−1y−1y====m(x−x1)−2(x−(−1))−2x−2−2x−1$$\begin{array}{rcl}{}_{\mathrm{}}& & {}_{\mathrm{}}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ & & \mathrm{}\mathrm{}\end{array}$$
2. Tentukan persamaan garis singgung kurva y=x2${}^{\mathrm{}}$ di titik yang berabsis (−2)$\mathrm{}$ !
   Jawab :
   • cari m dulu di absis x=−2$\mathrm{}$
     mm====f′(−2)2x2(−2)−4$$\begin{array}{rcl}& & {}^{}\mathrm{}\\ & & \mathrm{}\\ & & \mathrm{}\mathrm{}\\ & & \mathrm{}\end{array}$$
   • Bandingkan dengan soal no.1, disini kita belum punya y1$\mathrm{}$ sehingga kita cari terlebih dulu
     yy1===x2(−2)24$$\begin{array}{rcl}& & {}^{\mathrm{}}\\ & & \mathrm{}{}^{\mathrm{}}\\ {}_{\mathrm{}}& & \mathrm{}\end{array}$$
   • maka persamaan garis singgung kurva dengan gradien m=−4$\mathrm{}$ di (−2,4)$\mathrm{}\mathrm{}$ adalah
     y−y1y−4y−4y====m(x−x1)−4(x−(−2))−4x−8−4x−4$$\begin{array}{rcl}{}_{\mathrm{}}& & {}_{\mathrm{}}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ & & \mathrm{}\mathrm{}\end{array}$$
3. Tentukan persamaan garis singgung kurva y=2x2−3x$\mathrm{}{}^{\mathrm{}}\mathrm{}$ yang sejajar garis y=x$$ !
   Jawab :
   • cari gradien m dari persamaan garis lurus y=x$$ ingat y=mx+c$$ maka m=1$\mathrm{}$ , diketerangan soal, garis saling sejajar, maka m1=m2$\mathrm{}\mathrm{}$= 1
   • cari titik singgungnya (x1,y1)$\mathrm{}\mathrm{}$ ingat m=f′(a)${}^{}$ maka
     m14xx====f′(a)4x−341$$\begin{array}{rcl}& & {}^{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\\ & & \mathrm{}\end{array}$$
     x1=1$\mathrm{}\mathrm{}$ maka kita cari y1$\mathrm{}$ dengan mensubtitusi x=1$\mathrm{}$ ke y=2x2−3x$\mathrm{}{}^{\mathrm{}}\mathrm{}$
     yy===2x2−3x2(1)2−3(1)−1$$\begin{array}{rcl}& & \mathrm{}{}^{\mathrm{}}\mathrm{}\\ & & \mathrm{}\mathrm{}{}^{\mathrm{}}\mathrm{}\mathrm{}\\ & & \mathrm{}\end{array}$$
   • maka persamaan garis singgung kurva dengan gradien m=1$\mathrm{}$ di (1,−1)$\mathrm{}\mathrm{}$ adalah
     y−y1y−(−1)y+1y====m(x−x1)1(x−1)x−1x−2$$\begin{array}{rcl}{}_{\mathrm{}}& & {}_{\mathrm{}}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\\ & & \mathrm{}\end{array}$$
4. Tentukan Persamaan garis singgung pada kurva y=−2x2+6x+7$\mathrm{}{}^{\mathrm{}}\mathrm{}\mathrm{}$ yang terletak tegak lurus garis x–2y+13=0$\mathrm{}\mathrm{}\mathrm{}$ !
   Jawab :
   • cari gradien m dari persamaan garis lurus x–2y+13=0$\mathrm{}\mathrm{}\mathrm{}$
     ingat :
     ax+by=c$$ maka m=−ab$\frac{}{}$
     untuk x–2y+13=0$\mathrm{}\mathrm{}\mathrm{}$ maka m=−1(−2)=12$\frac{\mathrm{}}{\mathrm{}}\frac{\mathrm{}}{\mathrm{}}$
     keterangan soal garis saling tegak lurus, maka m1.m2=–1$\mathrm{}\mathrm{}\mathrm{}$
     m1.m2(12).m2m2m2====−1−1(−1).(21)−2$$\begin{array}{rlr}{}_{\mathrm{}}{}_{\mathrm{}}& & \mathrm{}\\ \frac{\mathrm{}}{\mathrm{}}{}_{\mathrm{}}& & \mathrm{}\\ {}_{\mathrm{}}& & \mathrm{}\frac{\mathrm{}}{\mathrm{}}\\ {}_{\mathrm{}}& & \mathrm{}\end{array}$$
   • cari titik singgungnya (x1,y1)$\mathrm{}\mathrm{}$ dengan m=−2$\mathrm{}$
     ingat m=f′(a)${}^{}$ maka :
     m−2−4xx====f′(a)−4x+6−2−62$$\begin{array}{rlr}& & {}^{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ & & \mathrm{}\end{array}$$
     x1=2$\mathrm{}\mathrm{}$ maka kita cari y1$\mathrm{}$ dengan mensubtitusi x=2$\mathrm{}$ ke y=−2x2+6x+7$\mathrm{}{}^{\mathrm{}}\mathrm{}\mathrm{}$
     yy===−2x2+6x+7−2(2)2+6(2)+711$$\begin{array}{rcl}& & \mathrm{}{}^{\mathrm{}}\mathrm{}\mathrm{}\\ & & \mathrm{}\mathrm{}{}^{\mathrm{}}\mathrm{}\mathrm{}\mathrm{}\\ & & \mathrm{}\end{array}$$
   • maka persamaan garis singgung kurva dengan gradien m=−2$\mathrm{}$ di titik (2,11)$\mathrm{}\mathrm{}$ adalah
     y−y1y−11y−11y2x+y−15====atau=m(x−x1)−2(x−2)−2x+4−2x+150$$\begin{array}{rcl}{}_{\mathrm{}}& & {}_{\mathrm{}}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ \mathrm{}& & \mathrm{}\mathrm{}\\ & & \mathrm{}\mathrm{}\\ & & \\ \mathrm{}\mathrm{}& & \mathrm{}\end{array}$$